If you’re feeling a bit lost, read this introduction to Bayes Theorem, which shows when and where to use the Math.

Comparing Two Hypotheses

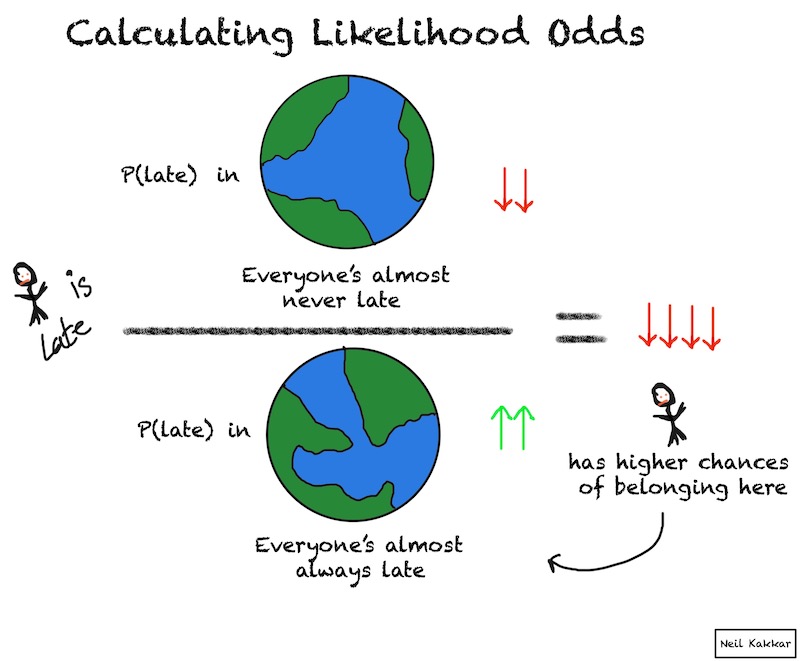
You’ve seen your colleague, Alice, be late 3 days, and on time 4 days the past week.

Hypothesis: They’re almost always late, i.e. they’re late 95% of the time.

Alternate Hypothesis: They’re almost never late, i.e they’re late about 5% of the time.

\[ Posterior \hspace{2mm} Odds = Prior \hspace{2mm} Odds * Likelihood \hspace{2mm} Odds\]

Main Hypothesis success rate %
Alternative hypothesis success rate %
Number of Successes
Number of Failures
Total
Likelihood Ratio (rounded)

Everyone has their own prior odds. I used 1:1 for the being late case. But, you can play around with these too.

Prior Odds :
Posterior Odds

In the being late example, this gives us that our current hypothesis is \(\frac{1}{19}\) times likely as the other one.

Comparing Two Hypotheses - known likelihoods

Prior Odds :
Likelihood Odds :
Posterior Odds

Comparing infinite Hypotheses

To come soon.

Have another use case I’m not covering? Let me know.

Interested in learning more?

Bayes Theorem: A Framework for Critical Thinking

This is a complete guide to Bayes Theorem for critical thinking. Learn why we think the way we do, and how we can do better. Everything arises from this simple formula from Probability Theory - Bayes Theorem.


You can send yourself an email with this post.