Bayes Theorem: A Framework for Critical Thinking
Have you ever noticed how you can be fuming with anger one second, and absolutely calm the next?
An asshole driver cuts you off on the highway, and you’re raging. A moment later, you notice him pull into the hospital and your anger melts away. “Yeah, maybe he has a patient in the car with him. Or, maybe someone close is dying. I guess he’s not an asshole after all.”
An obscure rule from Probability Theory, called Bayes Theorem, explains this very well. This 9,000 word blog post is a complete introduction to Bayes Theorem and how to put it to practice. In short, Bayes Theorem is a framework for critical thinking. By the end of this post, you’ll be making better decisions, realise when you’re being unreasonable, and also understand why some people believe in UFOs.
It’s a hefty promise, and there’s a good chance of failure. Implementing these ideas will take emotional effort, but it’s worth it.
Thinking the driver is an asshole is normal. Bayes Theorem expects the same. The difference between Bayes and us is the intensity with which we believe. Most times, the seething anger isn’t warranted. This is probably why we feel stupid about all that anger. It melts away so quickly! This is calibration - aligning our emotions to the intensity of the situation - which we’ll cover as well.
There’s no fancy math in this guide. We’re using Probability Theory, but aren’t going into the derivation, nor are we solving probability problems from school textbooks. These things are tedious without understanding the why. Instead, we’ll understand why Bayes Theorem matters, and how to apply it.
To begin with, let’s play a game. Throughout this game, notice how you feel about your decisions. Notice what decisions you’re making, and notice how you find the answer.
The 2,4,6 game
There’s a black box with a formula inside for generating 3 numbers. Your job is to try and guess this formula. The input box below is connected to the black box. If you give it 3 numbers, it’s going to tell you whether they follow the formula or not. Separate each number with a comma.
To start you off, (2,4,6) follows the pattern. Try it out!
Did you figure it out? Write down your answer in here:
Bayes Explanation
Most people try some sequence of: (4,6,8), (1,2,3) … and end up with either increasing numbers, or increasing numbers that are even. Notice how you’re pretty confident in your answer by the time you write it down. You’ve tried a few examples, and all of them made sense!
But perhaps you didn’t think to try (-1,2,10) or (4,2,6).
If my comment made your confidence waver, go ahead and try the input box again. See if you can find a pattern that works. The answer is at the bottom of this section, but don’t skip ahead. Every sentence before that is setting up an important idea.
Bayes Theorem
If you’ve heard of Bayes theorem before, you know this formula:
\[ P(H \mid E) = \frac{P(E \mid H) * P(H)}{P(E)} \]
Indeed, that’s all there is to it. I bet you’ve also heard the famous formula: \(E = mc^2 \). That’s all there is to mass-energy equivalence. However, figuring out how to harness nuclear energy is still a hard problem. The formula made it possible, but implementing it still took 40 years.
It’s the same with Bayes Theorem. The formula is exciting because of what it implies. We’re discovering the nuclear energy version of Bayes Theorem.
Translated to English, the formula goes like this:
To form accurate beliefs, you always start from the information you already have. You update beliefs. You don’t discard everything you know.
The first key component is a hypothesis (H) - the belief we’re talking about.
The second key component is the evidence (E) - what data do we have to support / reject the hypothesis.
The third key component is probability (P) of the above two. This probability is our confidence in the belief.
If you’re familiar with probability theory, you learned this in school. If not, don’t worry, there are excellent mathematical introductions to explain it to you. We’ll skip the math, and focus on how to use it.
Our point of interest, and where bayes truly shines is where we compare two hypotheses. Instead of uncovering the absolute probabilities, which is hard, this focuses on how much more likely one hypothesis is, compared to another. Most reasoning in our mind takes this form.
In this case, the formula looks like:
\[ Posterior \hspace{2mm} Odds = Prior \hspace{2mm} Odds * Likelihood \hspace{2mm} Odds \]
Posterior odds measure how likely a hypothesis is compared to another one.
Prior odds measure how likely it was before we had any new evidence.
Likelihood odds measure how well the evidence explains the current hypothesis, compared to the other one. We’ll explore what this means with the help of examples.
\[ \text{Likelihood Odds} = \frac{ \text{Probability of evidence assuming hypothesis is true}}{\text{ Probability of evidence assuming competing hypothesis is true}}\]
We’ll start with the 2,4,6 game to show how qualitatively, math and intuition agree. Then we’ll get into a simpler example where we’re miscalibrated and do the math.
I’m going to choose my path through the 2,4,6 game, but I hope yours was similar enough. If not, try doing this on your own!
I have a hypothesis I want to test, \(H_{3even}\) = 3 even numbers in increasing order. It’s implicit here, but the hypothesis I’m testing this against is \(H_{not-3even}\), or that the formula is not 3 even numbers in increasing order.
I input (4,6,8) and the black box says “Yes”. My confidence in 3 even numbers rises. In Bayesian-speak, my posterior odds have increased, because the likelihood odds have increased. And the likelihood odds have increased, since the probability of (4,6,8) saying “Yes” is higher when the formula is \(H_{3even}\).
You’ll notice how you feel every new number that matches your hypothesis makes your belief stronger.
I try (1,2,3) next. “Yes”. What? I expected “No”!
Everything tumbles, like it should, when you find something that doesn’t follow the pattern. The probability of (1,2,3) saying “Yes” is higher with \(H_{not-3even}\), since (1,2,3) are not all even. The likelihood odds are in favour of \(H_{not-3even}\) now, which means we discard \(H_{3even}\). In this case, one small piece of evidence was enough to completely flip the scales.
Then, which new hypothesis should you try? The clues usually lie in how you disproved the previous hypothesis.
I tried (1,2,3) which said “Yes”, when I expected it to say “No”. My new hypothesis thus became “3 increasing numbers”.
Just like in the previous case, (4,2,6) saying “Yes” killed this hypothesis. My new hypothesis thus became “3 positive numbers”.
I tried (-1,2,3), which said “No”! This was all I needed to become reasonably confident in “3 positive numbers”. The more negative numbers I tried, the more confident I got.
3 positive numbers is indeed correct.1
Graphically, this is what’s happening with the 3 hypotheses:
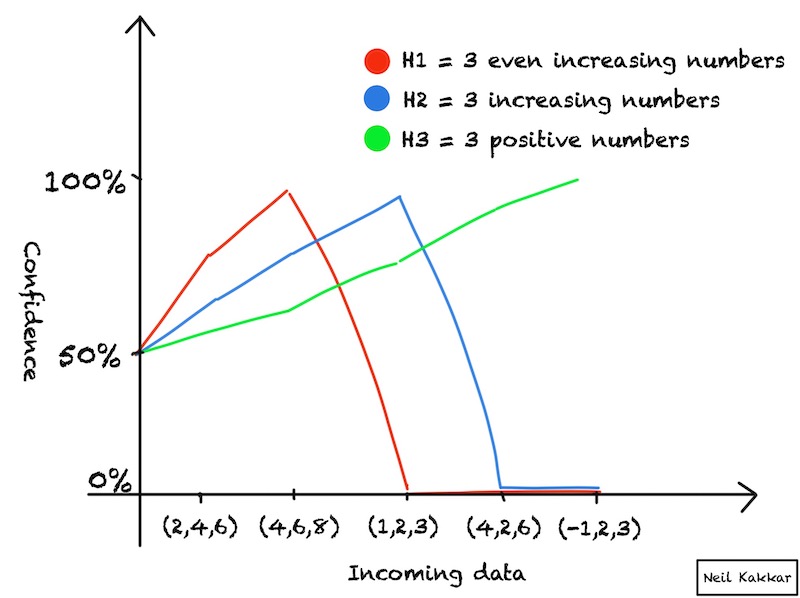
confidences not calibrated
Blue Box on Can we prove something to be true with Bayes?
No matter how much data you have, you can never say something is true. This is the problem of induction.
“No amount of observations of white swans can allow the inference that all swans are white, but the observation of a single black swan is sufficient to refute that conclusion.”
However, after a certain level of confidence, you live your life believing it’s true. Once you start believing is when you must pay close attention to evidence that doesn’t fit.
Calibration is key. What we’ve just shown is our thinking process, and how Bayes theorem is mostly aligned with it when we’re thinking well. Bayes theorem updates beliefs in the same direction our brains do, but what changes is how much each piece of evidence influences us!
With this next example, let’s get into the basic math. We’ll revisit the 2,4,6 game in a bit.
Being Late Example
Your colleague is sometimes late to work. They’ve been on time 4 times, and late 3 times the past week. How many more times would it take you to start believing they’re “always” late?
In my experience, just a few more times does the trick. But let’s use Bayes to calibrate.
Since there’s no good reason to expect tardiness over punctuality, let’s say the prior odds are 1:1.2 The alternative hypothesis, the one we’re testing against is “not always being late”. To make this more concrete, let’s say this means they’re late only 10% of the time.3
We’ll use the data we have to calculate the likelihood of being late. We want to contrast the databeing late thrice, and on time 4 times with us believing that they’re almost always on time, or almost always late. Remember, to figure this out, we imagine believing the first hypothesis, then judge how likely the data is. Then, we imagine believing the second hypothesis, and judge how likely the data is.
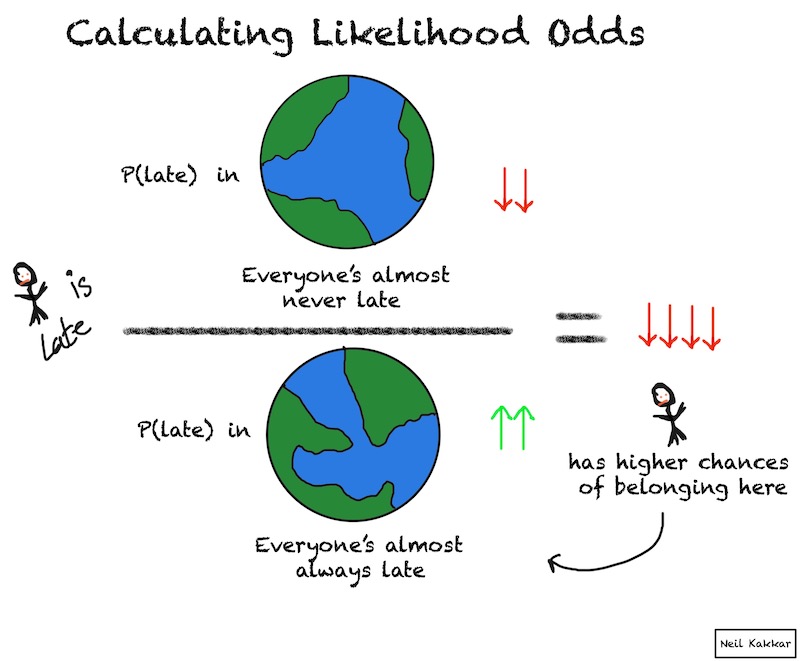
There are several ways to mathematically represent this data, from a binomial function to a beta distribution. However, we’re not getting into that yet. Today is more about an intuitive explanation, one which you’re more likely to use everyday. So try to imagine the odds for and against given this data.4
It’s a bit surprising to me that for someone who’s supposed to be always late, they’re on time more times than not. So this evidence is pretty unlikely for our hypothesis, while much more plausible when they’re not always late. I’ll give it likelihood odds of 1:10.5
Now, the posterior odds are \(1:10 * 1:1 = 1:10\). So, they’re 10 times less likely to be late than not.6
Huh, that’s surprising, isn’t it? Much lower than I imagined.
Let’s take this example further. Say we want to figure out how many more times would they have to be late to get the odds up to 100:1 ?
We’ll do the same updating process again.
Prior odds = the old posterior odds = 1:10 for being late.
Likelihood ratio = ??
Posterior odds = 100:1
Thus, likelihood ratio = 100:1 / 1:10 = 1000:1. Which means, they’ll have to be late for 12 days out of 20 to get these kind of odds.7
These numbers might feel weird. They are. We’re not used to calibrating, and in this specific case, we’re comparing two extreme hypotheses, which makes things weirder. Usually, this is a case of “I don’t know what the numbers mean”. We’ll explore this unsettling feeling in a bit.
Neither hypothesis is close to what we’d expect anymore. After all, the colleague is late just 12 out of 20 days!? Why aren’t we considering another hypothesis - say, they’re late 60% of the time? Try this hypothesis out, it should blow the other 2 out of the park. You can use this calculator I built.
For now, note that a little math helps us calibrate vastly better for the hypothesis we do have. It puts our emotions and thoughts into perspective.
Also notice how we transformed the problem to become easier to grasp. Instead of applying the complicated version requiring pen and paper (what are the probabilities, what are the formulas, how do I find them?), we follow this “old odds times current likelihood equals new odds”.
\[ Prior \hspace{2mm} Odds * Likelihood \hspace{2mm} Odds = Posterior \hspace{2mm} Odds\]
When you have this model explaining how the “ideal you” thinks, you get a gears level understanding! This is epic because you can fiddle with the gears and see how your thinking changes. You can figure out best practices, and become a stronger thinker. This is exactly what we’re going to do next.
Note:
The mind doesn’t always work like Bayes Theorem prescribes. There’s lots of things Bayes can’t explain. Don’t try to fit everything you see into Bayes rule. But wherever beliefs are concerned, it’s a good model to use. Find the best beliefs and calibrate them!
Grinding the Gears
Let’s start grinding these gears. A meta-goal for this section is to make the gears visible to you. We are inching closer to the nuclear energy version of Bayes Theorem, but so far we’ve just seen how it’s possible. The next step is to learn how to do it ourselves.
Using Bayes Theorem, try to answer this question:
How can two people see the same things and reach different conclusions?
Let’s first assume they’re Bayesian, and follow the rules. Can they reach different conclusions?
Yes! The current data only gives us the likelihood odds. There’s a second component, the priors, that are yet to be used! In the “being late” example, we thought them up using our background knowledge. This is why they’re called priors: it’s information we already have.
It’s plausible that two different people have different experiences, and different information. Which means, they can have different priors. Sometimes, these priors can get pretty strong. You, who has seen their colleague be late 3 out of 7 days will have different priors compared to Bob, who has seen their colleague be late 6 out of 10 days. Bob has seen your colleague be late twice as much!
Seeing your colleague be on time the following day would change your confidence a lot more than Bob. Can you figure out by how much?
For you = 1:20 (priors, 3 out of 7 days late) * (1:20) = 1:400 = 400x likely to believe their colleague is not “always” late
For Bob = 300:1 (priors, 6 out of 10 days late) * (1:20) = 15:1 = 15x likely to believe their colleague is “always” late
But, if both people are following bayes rule, they’ll both update in the same direction, and the same % amount - the one given by the likelihood ratio. That’s (1:20) in this case. Notice again how the numbers feel weird, like, this shouldn’t be correct.
The second case is when people aren’t following Bayes rule at all. Remember, Bayes is a prescription, not a description! Which means it’s how things ought to be, not how they are. This is where things get murky. It’s easy to spin evidence against a belief into evidence for. Especially if the hypothesis isn’t clear cut. We’ll get into this soon - just a few more ideas to attack first.
The 4 Rules for being a good Bayesian
Bayes Theorem has been around for 200 years, and in this time people have experimented with the gears to come up with best practices. Thanks to these people, we’ll explore 4 ideas driven from Bayes Theorem. Mastering these is key to becoming a better thinker.
Probability is a map of your understanding of the world
Ignorance exists in the map, not in the territory.
In this lens, the world is probabilistic. Everything has a probability of happening, based on your knowledge of the world. The probability is intrinsic to you, not the objects or situations.
For example, attacking in a gun fight might seem implausible to you, but mafia thugs would disagree. Your knowledge of the world determines your probabilities. These probabilities are your confidence in a belief.
Consider this seemingly weird example:
You meet a mathematician and she tells you she has two children. You ask if atleast one of them is a boy. She says Yes. You then decide the probability of both of them being boys must be 1/3.
You meet another mathematician. She tells you she has two children. You ask if the elder one is a boy. She says Yes. You then decide the probability of both of them being boys must be 1/2.
You meet another mathematician. She tells you she has two children. You ask if the younger one is a boy. She says Yes. You then decide the probability of both of them being boys must be 1/2.
If at least one of them is a boy, then either the elder or the younger one is a boy. So what gives? Why are the probabilities different? If the children had an inherent property of being boys, the answer should always be the same.
The probabilities are different because each question tells you something different about the world. Each question carries different amounts of information.
To resolve this paradox, we can draw it out. In the first case,

Notice how the question slices the possibilities differently than below. The first question removes only one possibility, GG, while the other two questions remove two possibilities, each.8
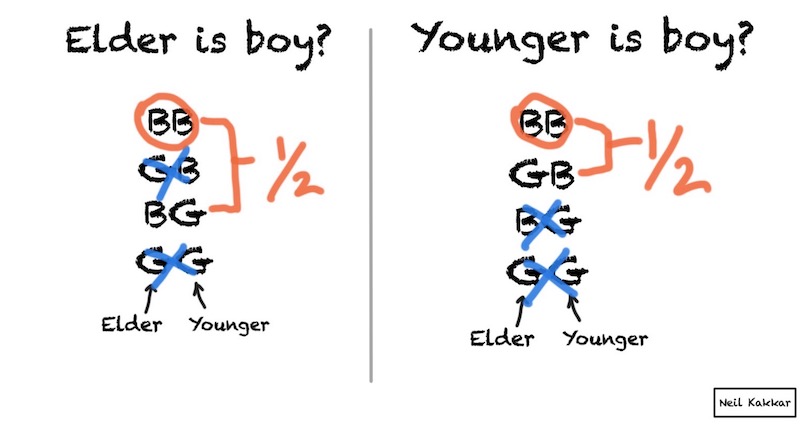
This same idea applies to figuring out your priors. It’s okay for different people to arrive at different odds because the probability is a function of the observer, not a property of the objects! Probabilities represent your beliefs and information. The sun has no probability, it’s you who believes it will rise everyday. And how much you believe can scale with the number of days you’ve been alive, or the number of days humanity has survived and recorded the sun, or if you believe the scientists and their methods - a few billion years. Of course, if you’re living near the North or South pole, your priors are bound to be different. Just because the sun exists doesn’t mean it rises everyday.
Probability lies in the eyes of the beholder
Update incrementally
Every extra piece of evidence changes your beliefs
In the 2,4,6 game your belief becomes stronger as you discover more evidence in favour of your hypothesis. The game is brutal: One failure and it’s game over for the hypothesis. This is a property of the hypothesis.Can you figure out what property? We’ll get to it soon
Real life hypotheses are usually not like that. Things are more fuzzy. Hence, your increments can tumble up and down depending on the evidence you find. In practice, this means not taking the newest evidence at face value. Always keep it in context with what you already know.
Like in the being late example, not updating incrementally would look something like: They’re late today, so I believe “they’re always late”. Notice how often you do this.
Of course, we’re not perfect at doing it wrong, either. If they’re on time instead, I’ll believe “Everyone is supposed to be on time. No big deal”, instead of, say, they’re always on time. This is called motivated reasoning.
“Evidence should not determine beliefs, but update them”
In the context of our examples, this seems very clear cut. Of course we’ll update incrementally. It would be dumb to discard all the information we’ve already acquired.
Here’s a more realistic example.
When I was 14, I heard how working out with weights can stunt your growth. I believed “Working out is evil and every big guy takes steroids”.
When I was 15, I heard how you can workout using just your body weight. That doesn’t stunt growth. I believed “Body weight workouts are amazing to get buffed”.
A few weeks later, with no gains, I was dejected. I believed “None of this works. It’s all a sham for corporations to make money.” I didn’t know who exactly was making money from my bodyweight workouts, but then again, I wasn’t a critical thinker.
Since then, I’ve done my own research. I understand how it’s a complex problem that depends not just on working out, not just on how long you work out, but also on what you’re eating.
I began updating incrementally. I took each piece of evidence in context with everything I had seen so far. Not everyone does steroids. Strength training works for at least some people. Intermittent fasting and running works for others. There’s no way, given all the diverse and contradicting evidence, that I can have close to 90% confidence in any belief about working out.
A sign of not updating incrementally is flip flopping between beliefs. You’re taking the evidence you’ve seen today as the complete truth.
Another failure mode is rehearsing your arguments. When one argument keeps coming back to your mind again and again, that’s a case of failing to update incrementally. You’re pitting the same evidence, which you’ve used already, to bloat up confidence.
A crude example of this is repeating to yourself “It’s going to be alright”, “It’s going to be alright” when facing a new risky situation. Sometimes, it’s necessary to calm your nerves. Other times, like the stock market bubbles, it’s you reinforcing a wrong belief when evidence points against it.
Seek disconfirming evidence
In a world where your pet theory is not true, would you expect to see something different?
In the 2,4,6 game, if you don’t test anything that you expect to be false, you can only ever find evidence in favour of your hypothesis. You can only become more confident in your ideas.
Disconfirming evidence is anything you don’t expect to fit in your hypothesis. In the 2,4,6 game these are situations where you expect the black box to say “No.” So, for the hypothesis “3 even increasing numbers”, (1,2,3) and (1,-1,2) are both possible disconfirming evidence.
(1,-1,2) shows you that your hypothesis, 3 even positive numbers might still be correct, while (1,2,3) shows you that it’s indeed wrong. You expected a No for (1,2,3) but got a Yes.9
In the being late example, disconfirming evidence for the “always late” hypothesis is looking for times when your colleague came on time. We tend to forget that, looking only at the times they were late. This leads to new problems.
Until you find disconfirming evidence and test your hypothesis, your beliefs are a castle of glass. And castles of glass are fragile. Indeed, the role of disconfirming evidence is to destroy castles, or make them stronger in the process.
The brain’s natural reaction is to protect this castle of glass. The brain views disconfirming evidence as attacks, and instead of being grateful, we tend to shut out the new evidence. If you dispel disconfirming evidence as rubbish, of course you’ll never change your mind. You’re always updating in favour.
You could input a million numbers that follow your pattern in the 2,4,6 game, and things would look good, but you’d never realise how your hypothesis is a subset of another (all positive numbers) - until one day your assumption fails you. There’s nothing Bayes can do about this.10
Thus, always seek disconfirming evidence. To do so, you can look for data that doesn’t fit your hypothesis, like we did above. The other way is to look for hypotheses that can better explain the data you already have. In Bayes-speak, you’re looking for hypotheses with better prior odds. Not all hypotheses are created equal. Some can explain the data better than others.
Julia Galef has a good example of this, tracking jealousy between friends. Just because Karen complains, doesn’t mean she’s jealous. Perhaps any reasonable person would do the same.
Remember your priors
Every moment you’ve lived is information you can use to figure out the next step
Last week, I woke up to a painful left eye. Even blinking hurt. It was swollen, and on closer investigation, I found something like a pimple inside my eyelid. I freaked out. “Holy crap, am I going to need surgery now? Will my eyesight be okay?!”
But, what if it’s just a pimple? It sure looks like one, but the first one that hurts. Maybe it isn’t that dangerous.11
I was panicking in the toilet, and then I noticed I was panicking. That was a cue for me to explore why. I did a quick mental calibration.
“I believe eye surgery to be 100x less likely than no eye surgery”. Most people I know haven’t gotten an eye surgery done. Except LASIK, which doesn’t count. In fact, even when I scratched my eye as a kid, it recovered without surgery.
“The pimple has 5x the odds of eye surgery than no pimple”. I’m not a doctor, but this sounds reasonable to me.12
Thus, in effect, odds for getting surgery are \((1:100) * (5:1) = 1:20 \). I’m 20x likely to not have eye surgery. Huh. Not too bad.
This happened quickly. These odds I calculated are the posterior odds! The prior odds were (1:100) and the likelihood odds (5:1). If I had discarded my priors, and only considered the new information I got that day, I’d be panicking at the (5:1) odds for surgery.
A few google searches once I was off the toilet helped confirm my estimates. I was still overestimating the danger. Styes are common and aren’t dangerous.
These posterior odds have now become my new priors. Next time, I’d be pissed, not panicking.
This story has an interesting insight: When we’re facing something new, our priors are usually miscalibrated. Taking the time to think through it can help put things in perspective. Remember your priors.
In some circles, this is also called Base Rate Neglect. You want to start a startup, and you think you’ll be successful because you’re awesome, you’re smart, and you’re hard working. What most people fail to realise is that so were most other start up founders! Yet, 90% of startups fail. Remember your priors.
On the flip side, don’t get too stuck on your priors. When new data comes in, remember to update incrementally. Being “set in your ways” is a criticism, not a compliment.

These 4 ideas together form the basis of good Bayesian thinking. The formula itself can’t think for you. It can just do its best with all the inputs you hunt down for it.
Even then, there’s lots of tricks our mind falls for, famously called “The Cognitive Biases”. Almost all of these are about incorrectly applying Bayes Rule, fudging with the inputs, or misunderstanding the outputs.
Destroying cognitive biases
Since Bayes Theorem is a basic framework for critical thinking, you can try it against some well known cognitive biases. These are times when we fail to think well. The strength of this framework depends on how well it can explain the biases.
-
Availability Bias: The tendency to overestimate the likelihood of events with greater “availability” in memory
= Using the evidence most readily available to you
= Discarding your priors
= Not updating incrementally -
Halo effect: The tendency for a person’s positive or negative traits to “spill over” from one personality area to another in others’ perceptions of them
= Using evidence for a different hypothesis as proxy for another
= Updating the wrong hypothesis
= Answering an easier question -
Dunning Kruger effect: The tendency for unskilled individuals to overestimate their own ability and the tendency for experts to underestimate their own ability
= Not seeking disconfirming evidence
-
Confirmation Bias: The tendency to search for, interpret, focus on and remember information in a way that confirms one’s preconceptions
= Not seeking disconfirming evidence
-
Base Rate neglect: The tendency to ignore general information and focus on information only pertaining to the specific case, even when the general information is more important
= Forgetting your priors.
This is very cool, but it is all post-facto. I know the bias, so now I know which part I misused. Can I figure this out apriori? Before I’ve made the mistake? That would be huge. Indeed, that’s something we’ll tackle a few sections below with the brain compass.
And of course, there are some which we have no idea how to explain:
-
Self-serving bias: The tendency to claim more responsibility for successes than failures
-
Outgroup homogenity: Individuals see members of their own group as being relatively more varied than members of other groups.
-
Cheerleader effect: The tendency for people to appear more attractive in a group than in isolation.
In summary, almost every social bias, ever. You can try out a few more from the list on Wikipedia
Seeking disconfirming evidence for Bayes
Applying the same ideas to Bayes Theorem, what can it not explain? Where do we expect Bayes to not work? That’s an opportunity for a better model to take its place.
We explored this in the cognitive biases section. Bayes can’t explain every bias, which means, at minimum, Bayes Theorem is not a complete model for how to think well.
The biggest gripe against Bayes is in scientific research. The Frequentists claim that the priors are subjective - too personal to drive at any objective truth. You need to see things happen, and assign probabilities based on how frequently they occur. The probabilities are a property of the object, not of your beliefs.
This argument is tangential to what we’re talking about. I don’t care about objective truths today, I want to focus on why we believe what we believe and how can we change *our* beliefs. Changing the entire world’s beliefs is the next step - too far away, too intractable, when I haven’t gotten a grasp of my own beliefs. I anyway mention this argument to keep us grounded.
For personal beliefs, it might seem (and will in the following sections) that I’m pulling numbers out of my ass and calling them the likelihood odds. That’s a fair question. However, arguing over the likelihood and prior odds is easier than arguing over statements in English. You can discuss which factors increase and decrease the likelihood odds, and have a fruitful discussion over why people believe what they believe. Contrast this with “You’re wrong! No, you’re wrong! Because X, Y, Z. Ha! That’s wrong too!”
The bigger gripe for us is that it’s hard to figure out all hypotheses - which means it’s very hard to know for sure your belief is right or wrong. This is a problem anyway. It’s important to note the relativity of wrong here - some things are more right, and more wrong than others.
When people thought the earth was flat, they were wrong. When people thought the earth was spherical, they were wrong. But if you think that thinking the earth is spherical is just as wrong as thinking the earth is flat, then your view is wronger than both of them put together - Isaac Asimov, Relativity of Wrong13
Not being able to figure out the absolute truth is no reason to not move in the right direction.
For us, we ought to use whatever we can learn, whether it comes from Bayesianism or frequentism. When you can count how many times an event has occurred to calibrate your priors, do. “Us vs Them” has no place in Bayesian thinking.
The 2,4,6 Game Revisited
Tip: This section, and the following one explore a lot of nuance. If it gets too heavy, skip to the Getting Stronger or learning to put it to practice section!
There’s one thing I left out during the 2,4,6 game analysis. The math.
It’s qualitatively different from the being late example, since just a single piece of evidence was enough to completely destroy the hypothesis. Can you guess why this is the case?
It’s a quality of the hypothesis. Some hypotheses are more specific and certain than others, and thus evidence increases and decreases a proportional amount.
Let’s say you’re testing out the hypothesis - “The Earth is flat”. What you see everyday raises your confidence in this hypothesis. The Earth is flat as far as you can see. The sky is up, the ground is down, and the sun moves from one edge to another. But, as soon as you see a video of Earth rotating from space, this hypothesis dies.
This is synonymous to us trying out (2,4,6), (4,6,8), (8,10,12) and gaining confidence, while crashing and burning with (1,2,3).
We are at the extremities of probabilistic reasoning, where instead of being uncertain, our hypotheses have 100% certainty. No room for error. If we can’t tolerate errors and uncertainties, we’re back in the world of logic. The spectrum from 0 to 1 dissolves into just two binary options: 0 or 1.
This “no room for error” is inherent in the hypothesis.
“The Earth is flat”, The formula is 3 even increasing numbers”, “He is always late”.
Sometimes, our language hides our implicit assumptions. Uncovering those, I can rewrite the above three like:
“The Earth is flat 100% of the time”
“The formula is 3 even increasing numbers 100% of the time”
“He is late more than 95% of the time”. This specific hypothesis is a bit tricky. When we say “always” late, we don’t mean always. Taken literally, being on time even once would crush this hypothesis. This is ambiguity we’ve got to be careful about when talking in language instead of math.
So, we’ve uncovered one quality of these hypotheses: They have a frequency attached to them. But, what about hypotheses like “I’ll be a billionaire” or “Trump will be president next election” or “I’ll need surgery for my eye”?
There’s no frequency here. It doesn’t make sense to say I’ll be a billionaire 100% of the time. You don’t get extra lives or parallel universes to test this hypothesis out. It happens once, and then you’re done. All we have is our confidence in the hypothesis, which we update when we find new data, according to Bayes rule.
In summary, there are 2 kinds of hypothesis: those based on a frequency of something happening, and those without. Frequency makes sense when you can repeat an experiment. Both kinds have confidence levels, which we update using Bayes rule.
Coming back to the 2,4,6 game, let’s now demonstrate all the details involved in an update. Our hypothesis is: The formula is 3 even increasing numbers 100% of the time. We’re comparing against “the formula is not 3 even increasing numbers (100% of the time)”.
With (4,6,8), I’d say likelihood odds are 2:1 for 3 even increasing numbers. I end up with posterior odds of 2:1.
With (10,12,14), the same story. Posterior odds now become 4:1. I’m getting pretty confident in this castle of glass.
A few more pieces of confirming evidence, like (12,14,16), (6,8,10) and now I’m up to 16:1.
With (1,2,3), the likelihood odds are 0, since it’s not 3 even increasing numbers. Posterior odds become 0, too.
Whenever the hypothesis has a 100% frequency, a single counter example is enough to destroy all confidence. It’s the land of no uncertainty. The extreme case for Bayes Theorem.
There should probably never be a hypothesis in which you have 100% confidence
Notice how I made even this hypothesis uncertain by adding the “probably”.
The Being Late Example Revisited
We have one final property left to uncover. This is the weirdness we faced while doing the math. But before that, let’s explore the new frequency property we just learned.
This cool graph should help prime your intuition. There are 5 lines, each of which is a different hypothesis: from late 0% of the time to late 100% of the time. In every case, the data we get is the person being late 4 days in a row, then on time the 5th day. Priors update everyday. I used the accurate math calculations for this graph, to show how exactly the calibration works with specific hypotheses.
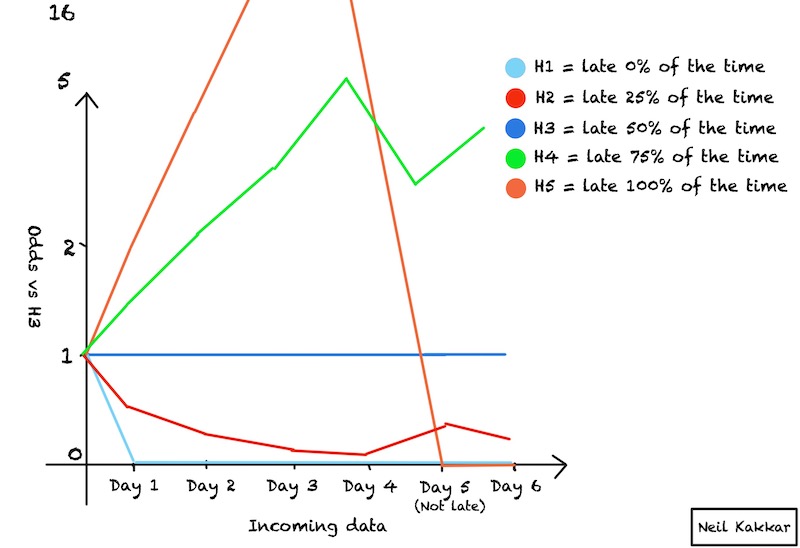
Compare this being late example to the stye in my eye example. What were the possible hypotheses for the stye in my eye? Either I need surgery, or I don’t. It’s a hypothesis without frequency.14 Being late, on the other hand, are thousands of hypotheses with varying frequency: My colleague is late 5% of the time, or maybe 10% of the time, or maybe 50% of the time, or maybe 80% of the time, or maybe 95% of the time.
You’re not just comparing two hypotheses - late 95% of the time vs late 5% of the time, but the entire universe of hypotheses. The (2,4,6) game also had lots of possible hypotheses, but we didn’t face this problem because of two reasons. First, there was no easy way to parametrize the hypothesis. We couldn’t just increase or decrease a number to create a new hypothesis. Second, all the hypotheses had 100% frequency and would die quickly, with just one counter example. New hypotheses would uncover themselves thanks to the disconfirming evidence.
Here, the hypotheses are on a spectrum. In such a case, sometimes you’re more interested in figuring out what the frequency with the highest confidence is. For the math nerds, and for those who will continue learning about the math: this problem is called parameter estimation. In effect, you’re short-circuiting comparing 2 hypotheses, by comparing all of them together, and settling on the one with the highest confidence.
A good rule of thumb here is to choose the mean. If you’ve seen someone be late 12 out of 20 days, the hypothesis with the highest confidence level would turn out to be the one with the same frequency: 12/20 or 60% of the time. This is why I claimed earlier that the 60% hypothesis would blow the 95% hypothesis out of the park. This was a new hypothesis being uncovered thanks to the data.
Indeed, if you used the calculator or did it yourself, likelihood odds in favour of being late 60% of the time is 67,585 to 1. Similarly for being late 5% of the time, likelihood odds in favour of 60% of the time is 8,807,771,533 to 1. Remember, 95% of the time had 130,000:1 odds vs late 5% of the time. If you divide the two above, you get the same odds.
This also answers the numbers looking weird feeling we had earlier. We were comparing 95% to the 5% hypothesis, and 95% won by a huge margin. But at the same time, a hypothesis we didn’t know about, the 60% blew both of them out of the park. It felt weird because 95% seemed like the best, when the data clearly pointed in a different direction.
This should give you a good idea of how learning the math can be worthwhile. Once you’ve ingrained the habit for thinking like a Bayesian, the next step is calibrating better with Math. But there’s two more things you can do before that, which are up next.
Getting stronger
Following Bayesian Thinking is hard. It’s counterintuitive to reason about things you’re used to feeling out. In most day-to-day low risk situations, you probably don’t even need it. But, the way you prepare yourself for the few times a day you do need it is by practicing on the low risk situations.
This section looks at what you can do, and the next section focuses on practice.
Improve your priors
Experience is an exercise in improving your priors.
Read widely, learn about things you don’t know exist. If you’re trying to improve your thinking in a specific field, go broad within that field. Figure out what all can happen and how frequently it happens.
Sometimes, numbers can help a lot. For example, this cheatsheet for engineers is very famous, and I visit it often - whenever I’m building new systems, or reasoning about timing bugs. It gives me a more realistic idea of how slow or fast things can be, precisely because my priors are shit! A very experienced engineer could tell without looking, precisely because they have better priors.

Someone heard this same tip and went on to create better systems. In Bayesian-speak, they improved their priors. I’d go further: Experience is an exercise in improving your priors.
Become a master hypothesis builder
You can’t test the idea if you don’t have the idea in the first place.
Using Bayes Theorem depends a lot on the hypothesis you’re testing. If you’ve ever noticed yourself trying the same thing again and again, without progress, your hypothesis generating machine has stalled. You can’t come up with an alternative explanation, so you end up trying the same thing again.
This can get painful.
The alternative is to become a master hypothesis builder. An idea machine. Train yourself to think of alternating view points, different ways to explain the same thing, and different things you can try to fix them.
Your beliefs can only be as accurate as your best hypothesis.
The more ideas you can surface, the more ideas you can try, and the better your chances of winning! Like we saw in the being late example, the 60% hypothesis may never come to you, and if you’re stuck with only the 95% and 5% hypothesis, you’re bound to be wrong.
However, that’s not all. Some hypotheses are better than others. As we’ve seen before, not all hypotheses are created equal. At the minimum, your hypothesis needs to be falsifiable. It needs to be clear cut. It needs to be specific enough. The hypothesis “anything can happen” is true, but not very useful. The inputs determine the quality of your output.
A good way to check the quality of a hypothesis is to decide beforehand what will convince you that your hypothesis is wrong. If the answer is nothing, that’s a bad sign. Remember, all our beliefs and convictions are hypotheses - and challenging our beliefs is a good place to try this out. What would convince you that climate change is real?
The remarkable thing about small children is that you can tell them the most ridiculous things and they will accept it all with wide open eyes, open mouth, and it never occurs to them to question you. They will believe anything you tell them. Adults learn to make mental allowance for the reliability of the source when told something hard to believe. - E.T Jaynes in Probability Theory13, pg 99.
A part of growing up is learning how to come up with hypotheses. Children learn from their mistakes. They soon learn the truth about Santa Claus, the neighbourhood monster, and the tooth fairy. They learn other people aren’t always the most reliable sources. This is step 1 of becoming a master hypothesis builder.
Here’s another example: In the 2,4,6 game, why didn’t you think of a hypothesis like: “It’s either (-2,-2,-2), or 3 positive numbers”?
Learn the Math
Math helps you calibrate better. Since our intuitions usually flip us up, it’s good to get grounded in the Math. I like to defer this step to the end, after you’ve put Bayesian thinking to practice.
Putting it all together in practice
I have one final analogy for you, tying everything we’ve learned together. This is why you’ve spent so long reading this monster blog post.
Like tradition so far, here’s a story to demonstrate the idea. This is Richard Feynman working through seemingly counterintuitive theorems:
I had a scheme, which I still use today when somebody is explaining something that I’m trying to understand: I keep making up examples. For instance, the mathematicians would come in with a terrific theorem, and they’re all excited. As they’re telling me the conditions of the theorem, I construct something which fits all the conditions. You know, you have a set (one ball) - disjoint (two balls). Then the balls turn colors, grow hairs, or whatever, in my head as they put more conditions on. Finally they state the theorem, which is some dumb thing about the ball which isn’t true for my hairy green ball thing, so I say, “False!”.
If it’s true, they get all excited, and I let them go on for a while. Then I point out my counterexample.
“Oh. We forgot to tell you that it’s Class 2 Hausdorff homomorphic.”
“Well, then,” I say, “It’s trivial! It’s trivial!”
I guessed right most of the time because although the mathematicians thought their topology theorems were counterintuitive, they weren’t really as difficult as they looked. You can get used to the funny properties of this [..] and do a pretty good job of guessing how it will turn out.
We can build a similar model for our reasoning!
Everything we’ve talked about reduces down to two exciting use cases for Bayes Theorem: figuring out the hypothesis with highest confidence so far and then calibrating well.
Imagine you are a compass. A brain compass.
You’re at the center.

Around you is all the possible data - things you know, expect, as well as things you know that you don’t know. It’s the disk of priors.
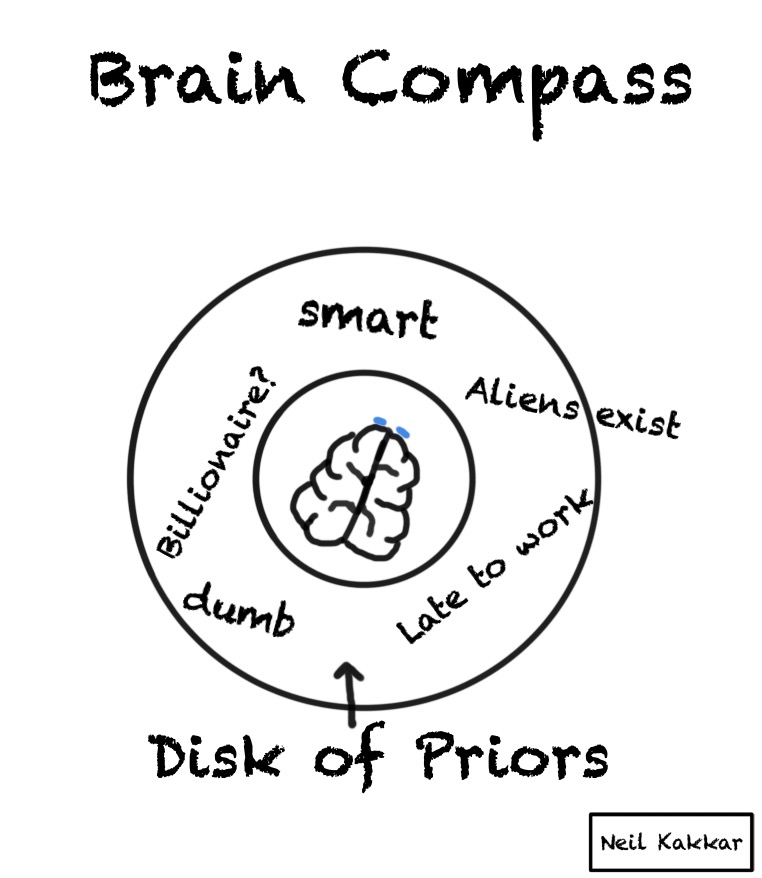
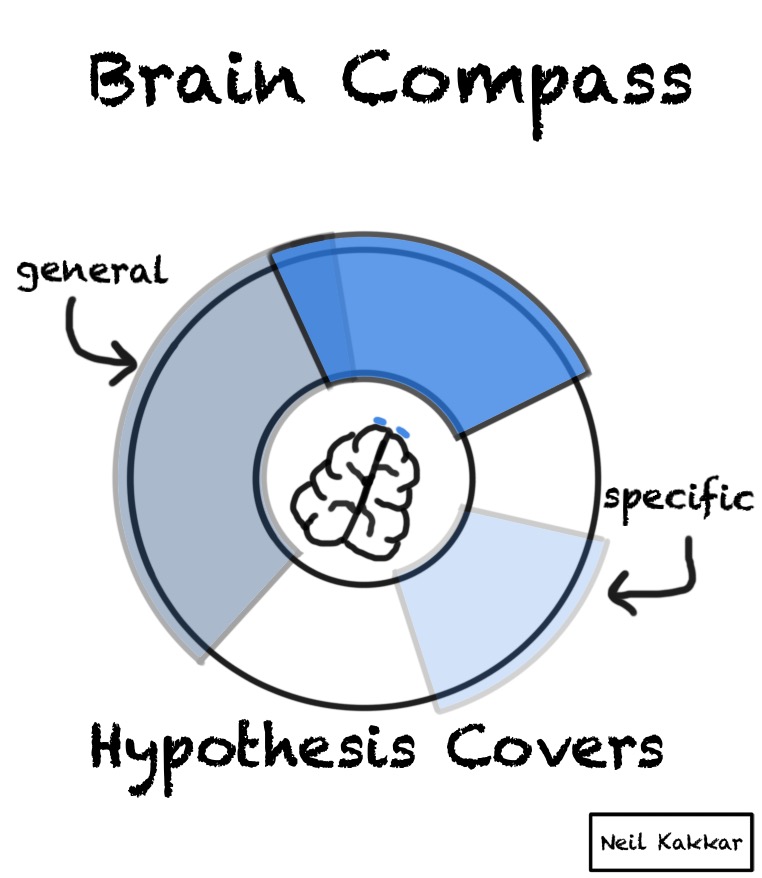
A hypothesis cuts this disk of priors into two parts - what you expect to happen, and what you don’t. The more specific the hypothesis is, the smaller the “truthy” section of the disk is.
The intensity of the colour is your confidence level in the hypothesis. The brighter the color, the higher the confidence.
But wait, you usually have several hypotheses. I like to think of the hypothesis as covering some part of the territory. Thus, I call the hypothesis, a hypothesis cover. There are several hypothesis covers, each with their own intensity, all placed around the disk.
Next is our evidence. Incoming data is balls falling on this brain compass. Imagine yourself taking this data in through your senses. Your senses package whatever you know and see into these balls of data.
Every ball becomes part of the disk of priors. It’s real world data merging with what we think is possible.
If it falls through a hypothesis cover to make it to the territory, the intensity of the hypothesis cover increases. This is us updating incrementally.
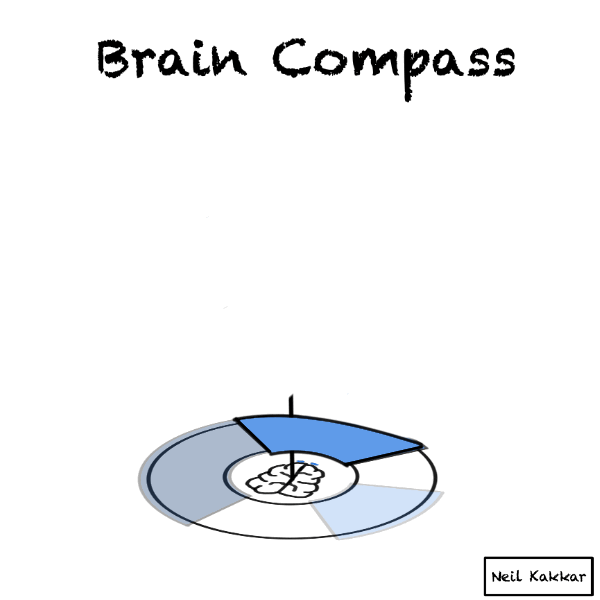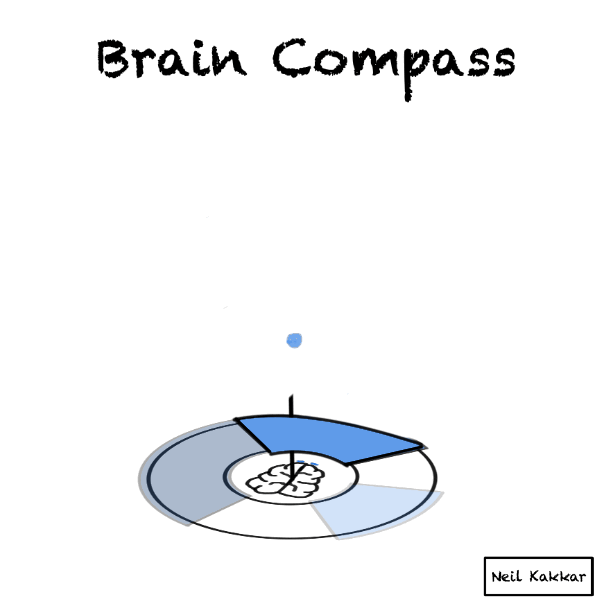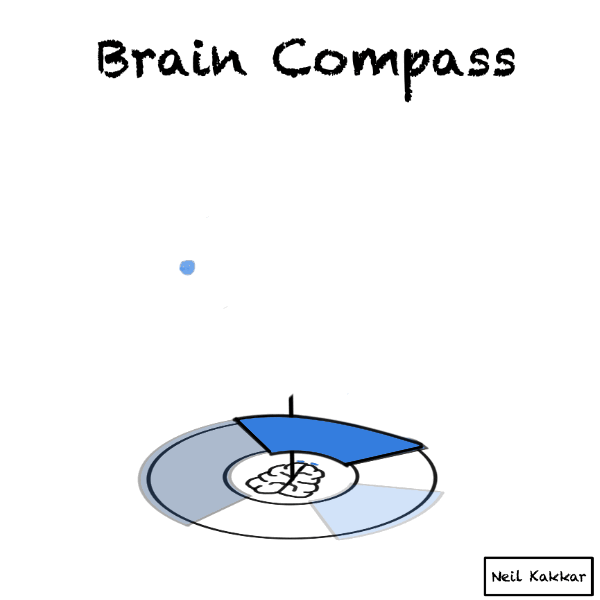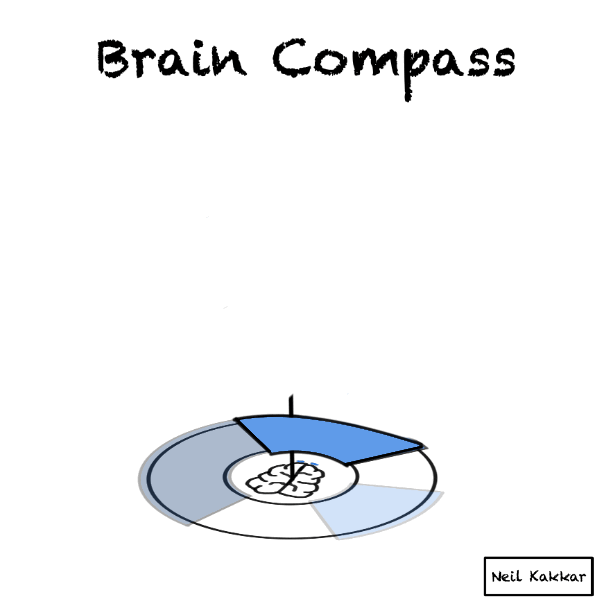
If we see all the balls falling into the hypothesis cover, it’s time to seek disconfirming evidence. Make sure some balls have the opportunity to fall outside the hypothesis cover!
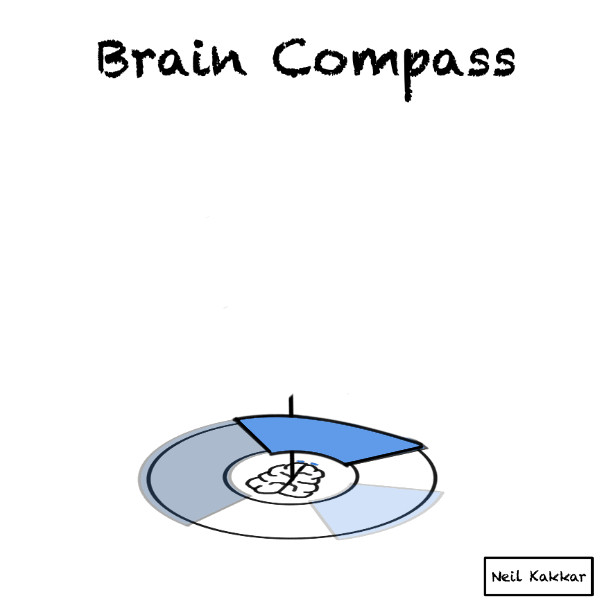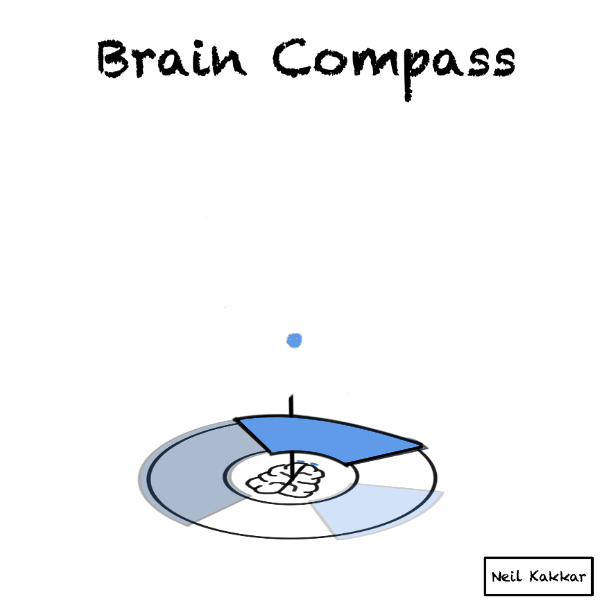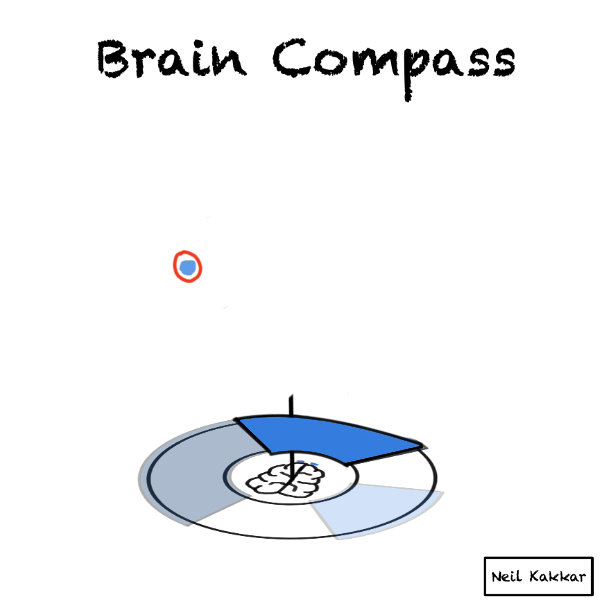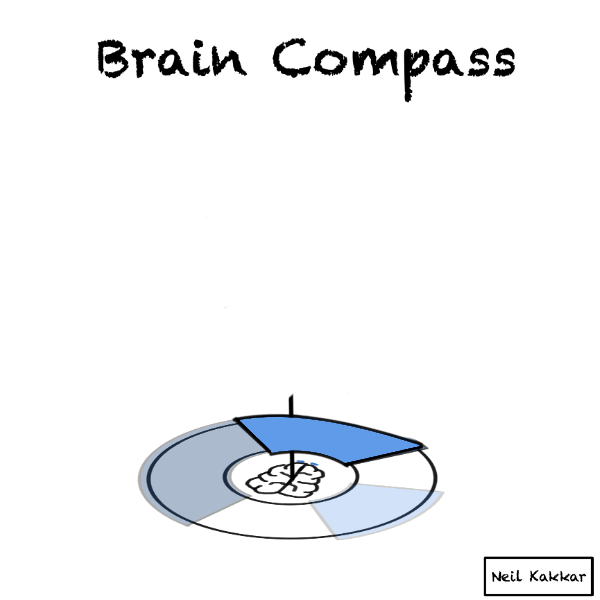
If every ball of data falls inside your hypothesis cover anyway, maybe your hypothesis is too general to be useful. “Anything is possible” will accept all the balls, but it’s not very useful. If you imagine the brain compass here, you’ll see that the hypothesis cover covers the entire territory!
This mental picture helps me remember how to use Bayes well. It visually shows me the difference between my priors and how much the hypothesis can explain. It’s a tool for thought, where the better I get at visualising, the better I get at using Bayes theorem.
To make things more concrete, lets walk through one example using the brain compass. Say, the hypothesis is “I’ll become a millionaire”.
In my mind, I immediately see a hypothesis cover saying “Neil = Millionaire”. This then triggers a search for priors. We usually start by thinking the hypothesis cover is the entire disk. Don’t stop there. Figure out the entire disk. Don’t discard your priors!

The hypothesis cover is “Neil = Millionaire”, and the rest of the disk is “Neil != Millionaire”. I then realise that incoming data can’t really fit into this. I can’t test whether I’m a millionaire or not in the future using just this, since I have 0 data.15
So, I change the domain. I start looking for data I can use today that reliably predicts millionaires. First, the disk of priors becomes the number of people who are millionaires vs those who aren’t. Hypothesis cover falls on the millionaires.
The incoming data is properties of these people. Who are hard working, lucky, etc. Balls fall both in the hypothesis and outside. Ratio falling inside is the likelihood ratio, and the hypothesis color darkens if the ratio inside is higher.
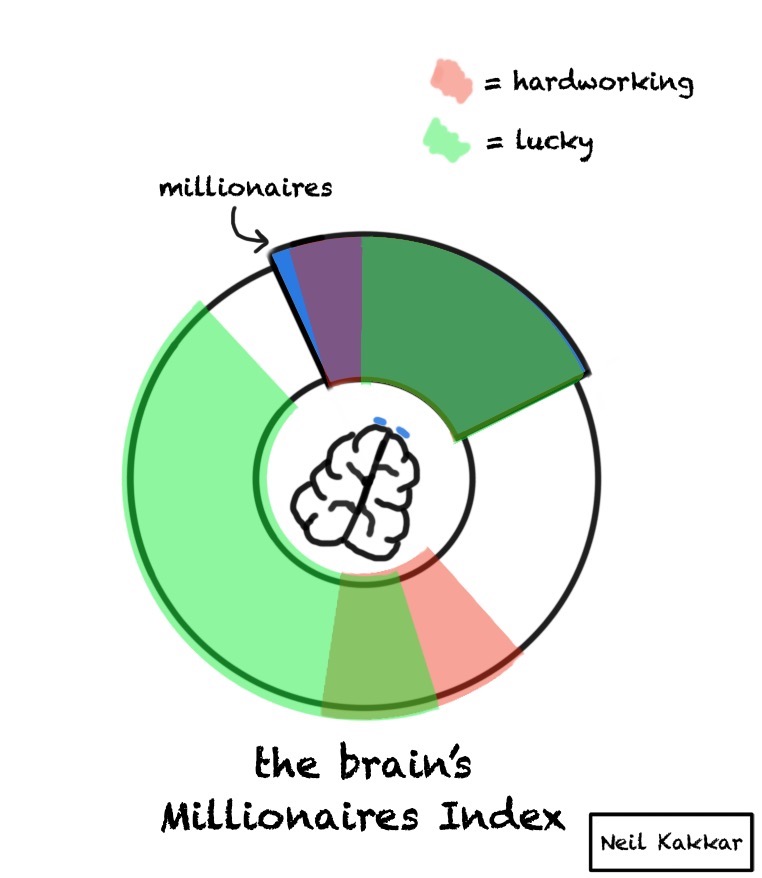
You’ll notice it’s hard to reason about this now, while without the brain compass, you could just use whatever ambiguous criteria you wanted to: “I’m smart, hard working, lucky, so I have very good chances of becoming a millionaire.” Now, you can see all the other smart, hard working, lucky people who aren’t millionaires.
The Brain Compass stops you from answering an easier question. Further, building the disk of priors forces you to think of not just the hypothesis cover, but what lies outside it. This also forces you to think of how big the cover should be. How much of the territory does it cover?
A good way to realise you’re messing up is when you can’t visualise the complete Brain Compass for your hypothesis.
There are trade-offs though. This brain compass visualisation isn’t as accurate as the Math. But it’s excellent for everything that comes before the math. I use it a lot more than I use the math, since with most decisions, I can live without the perfect calibration.
It’s more about building a tool for thought that warns you before you fall for the pesky cognitive biases. As you uncover new biases, you can incorporate them into your brain compass.
For example, you can visualise confirmation bias as looking for balls that only fall inside the hypothesis cover, and your brain throwing away the balls falling on the rest of the disk of priors. Perhaps in this case you can’t even see the disk of priors.
Slowly, you’ll start seeing the shape of biases in your brain.
Hypotheses with frequencies
It’s a bit hard to demonstrate, but things get a bit weird when dealing with hypotheses having frequencies. Say the hypothesis is my colleague is late 75% of the time.
When visualising this, some data points that fall outside your hypothesis cover will increase your confidence! I find it best not to try and calibrate using the brain compass in this case. I still use it to get to the point where I’ve collected some data, figured out my hypothesis, and now need to find confidence levels.
Growing the disk
Incoming data plays a second crucial role: Growing your disk of priors.
Increasing the size of the disk grows your mind. If everything you’ve seen gives aliens on earth a 100:1 chance of existing, perhaps notice the balls falling outside your disk. Grow the size to include those outside your model.
Surprise is something you didn’t predict, or something you didn’t even know existed! Mathematically they’re the same, but qualitatively, one’s revising your hypothesis, the other is broadening your disk of priors to what else is possible.
Switching hypotheses
It might be tempting to think of the hypothesis cover as a slider - You move it to wherever most of the balls are falling. But that’s not what actually happens. Looking at the brain compass from the top hides how the hypothesis covers are positioned.
Here’s a side view:
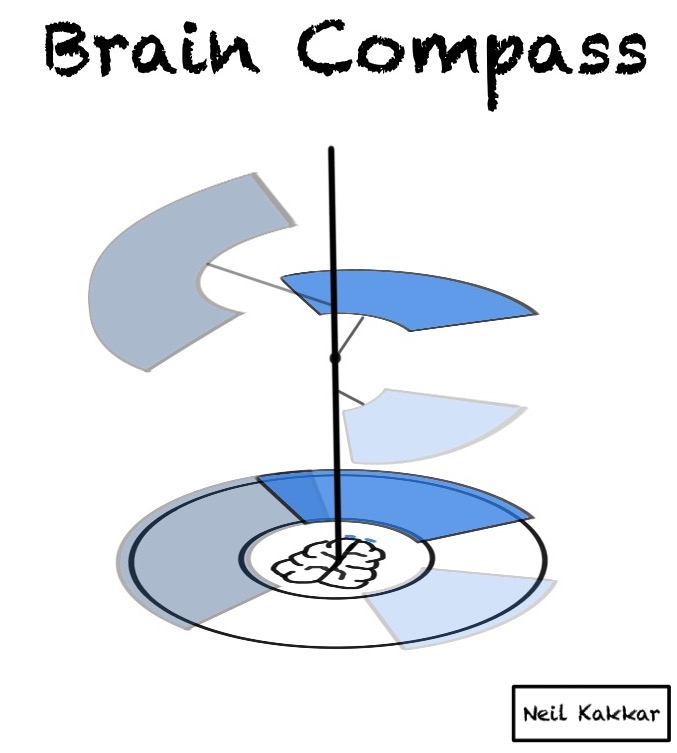
When data falls outside your hypothesis cover, your hypothesis begins fading. At the same time, wherever this data is falling brightens a hypothesis cover in that area. You notice every hypothesis that gets bright enough. This is similar to how, in the 2,4,6 game, whatever data destroyed our hypothesis gave us a hint to our next hypothesis.
At the same time, our beliefs are always the ones with the highest confidence. Taken together, this is how all 3 hypotheses in the 2,4,6 game look like:

Strong Opinions, Weakly Held?
As with every idea that makes it into pop culture, it gets simplified and re-interpreted to mean whatever the arguer is saying. I’d like to reframe this saying via the lens of the brain compass.
An opinion is a hypothesis cover. A strong opinion is a narrow cover. The narrower the territory, the stronger the hypothesis.
Weakly held means updating incrementally in the face of counter-evidence. Huh, that sounds a lot like something we know, doesn’t it?
A proper reframing would be “Strong opinions, Bayesianly held”. But I guess that’s not catchy enough.

There’s lots more examples we can reframe with the brain compass, but I’ll stop here.
This seems very different to what I learned in school
Go to any online introduction to Bayes Theorem, and here’s what you’ll see:
“You think being late to work has a 50% chance of happening. You know it depends on your alarm clock not going off in the morning. Your alarm clock didn’t go off. What’s the chance of being late to work now?”
Except, that’s not how we think.16 The funny thing is, when I first started writing this post 2 months ago, this was indeed the introduction. This framing is very useful for scientific hypothesis testing, but not if you want a quick and intuitive grasp for everyday life. You don’t have time to get your scientists notebook out and compute every time you want to use Bayes.
The way you achieve the intuitive grasp is by reframing. You transform the problem so your brain can grasp it quickly. For example, CPUs can do lots of calculations one by one very well. But when it comes to graphics, not only do we need to do lots of calculations, we need to do them in parallel so that we can see the entire screen render at the same time.17 Thus, we break the problem down and feed it to the GPUs in a way that’s easy to process. Parallel processing algorithms follow the same idea!
We broke up the parts of Bayes theorem, the hypothesis, evidence, and the priors - and reordered them in the way we intuitively think. See the footnote above16 for more details.
Epilogue: The End is the Beginning
To summarize, there are lots of subtle ideas we tackled. We started with the (2,4,6) game, realised how our thinking process was roughly Bayesian, and how we’re miscalibrated. We then figured out there are 2 kinds of hypotheses: those with frequency3 even increasing numbers 100% of the time and those without.I’ll become a billionare
Every hypothesis has a confidence level, which we update using Bayes theorem. Any hypothesis with a 100% frequency or confidence faces 1 hit KOs.3 even increasing numbers 100% of the time dies completely at (-1,2,3) When one hypothesis dies, another one takes its place. A master hypothesis builder has several of these ready to test. We always believe something, and we’d do well to believe the most probable thing given all the data we’ve seen so far, and our priors!
How we disprove our hypothesis is a hint for the next hypothesis. This is systematized by always seeking disconfirming evidence. Remember we can never prove something, only disprove. There’s always some uncertainty in our beliefs. But of course, this doesn’t mean we’ll go about believing the hypothesis that’s 1000x less likely. Some things are more wrong than others.The Relativity of Wrong
Bayes Theorem, and by extension Critical Thinking, is about finding the most probable beliefs, and then calibrating.
The next phase is figuring out better tools to more accurately map the territory.
-
Learn the math. Bayesian Statistics the fun way13 is an excellent book, and I can’t recommend it enough! Better tools help model reality better. A good next step from the book is the Beta Distribution, which helps model the entire space of frequencies for the being late example.
-
Learn why any model of thinking that is consistent and qualitatively in line with common sense must end up at Bayes Theorem. This is a lecture from ET Jaynes, on building a system of plausible reasoning. You can see all the other lectures too.
-
Notice why you believe what you believe. Notice how you reach conclusions. Notice when you jump to conclusions. Notice how that errors out for you. Cultivate The Art of Noticing.
Bayes Theorem won’t be useful if you forget to apply it when you need it the most. Not surprisingly, when you need it the most is when it’s most likely to slip out of your mind.
-
It’s also worthwhile to look at some cool applications of Bayes Theorem - it’s been used widely, from detecting cancer, email spam, to environmental damage. Check out the link on environmental damage - every paper has the formula somewhere at the top, but the part you’re interested in are the diagrams. This is a hypothesis with frequency, and we’re using beta distributions to model damage, which also leads to the rule of thumbChoose the mean: late 60% of the time when you’ve seen them be late 12 out of 20 days in the being late revisited example.
-
Learn about the Bayesian Model of the Brain (a.k.a Predictive Coding) in Surfing Uncertainty13. Scott Alexander also has an excellent book review.
Oh, and finally, for the 2,4,6 game, I know I said 3 positive numbers is correct, but it isn’t. Despite all our efforts, sometimes we fail to arrive at the right answers. But of course, as Isaac Asimov said, 3 positive numbers is less wrong than 3 even increasing numbers.
And in the end, that’s what critical thinking is: becoming less wrong.

Appendix: More Good Examples
Tried this out yourself? Send me an email / tweet with how it worked out for you and your Twitter/website. I’ll add your responses here.
Expand: Examples
So I started a new job 3 weeks ago. And I had a “honeymoon” period for the 1st week before reality struck me again.
Gaming company that is doing amazing financially in the COVID home-stay scenario.
My first week, people seemed so nice. Team was friendly and chill. The executive leadership team seemed surprisingly down-to-earth, relaxed, and low-key…dare I say, “rad!”. The team played video games together at 5 PM on Tuesday.
The 2nd week, things start to rapidly change. I start to notice typical office atmosphere, ambitious goals, overworked/fearful employees, stressed leadership, etc. This didn’t happen immediately, but through Bayesian updating and remembering to remember my priors. It took me 3 days – when it could have taken me 3 weeks if I had forgotten my priors.
Now – on the flip side, being too prior-focused can hurt you. It almost did for me. I almost didn’t notice all the unique positives that showed up at my new workplace –– if I had convinced myself that it was no different than my last job. Luckily, I reached out to my friends and asked for their opinions. I was willing to update my priors.
It’s like Neil says here, you gotta actively combat your own existing models that seek self-perpetuating confirmation. And seek alternate, good hypotheses

Thanks to Hung Hoang, Nishit Asnani, and Lloyd Xie for reading drafts of this.
-
Correct because I already know the formula. In a real life uncertainty situation, you’ll never be sure! Your confidence levels will keep inching towards a 100%, but never touch 100%. ↩
-
We’ll see a bit later where the 1:1 comes from, and how you can change it. ↩
-
We go into what these words mean in a following section. This is also why I have “always” in quotes. ↩
-
of course, the math is more accurate! When you have decisions to make with a lot riding on them, it makes sense to take the extra time and figure out what you can. This intuitive calculation is a first step that instills the habit. ↩
-
Mathematically, 1:10 is close to being late 90% of the time, and 1:20 is close to being late 95% of the time. ↩
-
If you’re familiar with the probability form of Bayes Theorem, this might seem weird. Check this explanation to understand the difference between odds and probability multiplication. ↩
-
The calculation here is based on the binomial distribution. I know, I said no fancy math. Here’s a calculator I built to do this yourself. I’m assuming 90% late for the main hypothesis, 10% for the alternate, and 12 successes, 8 failures. The odds should come out to 6,000:1 - I rounded that down to 1000:1. ↩
-
Here’s an in depth explanation ↩
-
(1,-1,2) is disconfirming evidence, too! Just that in this case, it failed to disconfirm your hypothesis. (You expected No, and got No) ↩
-
In this case, where the brain just can’t reject the results, the natural step is to blame someone else. Atleast the castle didn’t come down because of you. ↩
-
This was me trying to calibrate my sense of danger. ↩
-
This was me figuring out likelihood odds. ↩
-
There’s a way to formulate this problem as a hypothesis with frequency, but that becomes a different problem - and a different hypothesis. ↩
-
This is the difference between hypotheses with frequency and without! ↩
-
Did you figure out the difference between this formulation and how we usually think? This one’s starting with the priors! On the other hand, we start with the incoming data (the alarm clock didn’t go off), which raises the hypothesis - “Am I going to be late today?”, then adjust confidence according to our priors (50% chance of being late). ↩ ↩2
-
If you’ve ever seen a photo load slowly, part by part, that’s the CPU processing it layer by layer. Or a slow internet connection slowing the CPU down. ↩
You might also like
- How to setup duration based profiling in Sentry
- How to simulate a broken database connection for testing in Django
- The "People fuck up because they're not like me" Fallacy
- How I Own Projects as a Software Engineer
